减治法
减治(decrease-and-conquer)利用一个问题给定实例的解和同样问题较小实例的解之间的某种关系,
一旦建立了这种关系,我们既可以从顶至下,也可以从底至上地来运用该关系。
自底而上的版本往往是迭代实现的,从求解问题的一个较小实例开始,该方法有时也成为增量法(Incremental Approach)。
减治法有三种主要的变化形式:
- 减去一个常量:计算$a^n$的值,$a^n = a^{n-1} \times a$
- 减去一个常数因子: $a^n = a^{n/2} \times a^{n/2}$
- 减去的规模是可变的: 计算最大公约数的欧几里得算法,$gcd(m, n) = gcd(n, m mod n)$
插入排序
使用减一技术对一个数组 $A[0..n-1]$ 排序,
假设 $A[0..n-2]$排序的问题已经解决了,需要做的就是
在这些有序的元素中为 $A[n-1]$ 找到一个合适的位置,
然后将$A[n-1]$ 插在该元素的后面。

最差(输入为逆序数组)效率: $\Theta(n^2)$
最好(输入已经为升序)效率: $\Theta(n)$
平均效率(输入为随机序列):$\Theta(n^2)$
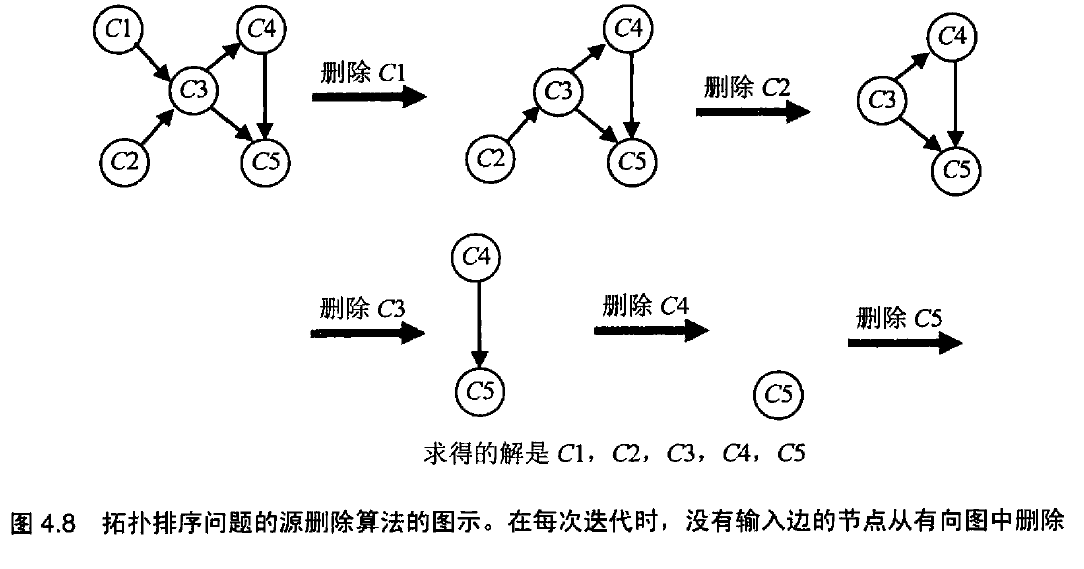
拓扑排序
问题定义:给定一个有向无环图,能否按照一定次数列出它的顶点,使得对图中每一条边来说,边的起始顶点总是排在变的结束顶点。
第一种算法:DFS遍历,并记住顶点退出遍历栈的顺序,将该次序反过来就得到拓扑排序的一个解。
第二种算法:基于减一技术,不断重复这么一个过程,在余下的有向图中求出一个源,它是一个没有输入边的顶点,然后把它和所有从它出发的边都删除。顶点被删除的次数就是拓扑排序问题的一个解。
拓扑排序在计算机科学中的应用,包括程序编译中的指令调度,电子表格单元格的公式求值顺序以及解决
链接器中的符号依赖问题。
生成组合对象的算法
生成排列
要生成$n$个元素的排列,可以假设已经生成了 $(n-1)!$ 排个列,可以把 $n$插入到 $n-1$ 个元素的每一种
排列的$n$个可能位置中去,来得到较大规模问题的一个解。
一般来说,都是,一开始从右向左把$n$插入 $1,2, \cdots (n-1)$ 的位置中,然后每处里一个 ${1, \cdots, n-1}$
的新排列时,再调换方向。
按照字典序生成排列的思路:如果 $a_{n-1} < a_n$ ,可以简单地调换最后这两个元素的位置,
如果 $a_{n-1} > a_n$ ,则需要找到序列的最长递减后缀 $a_{i+1} > a_{i+2} > \cdots > a_n$
然后把$a_i$与后缀中大于它的最小元素进行交换,以使$a_i$增大,再将新后缀颠倒,使其变成
递增排列。

生成子集
减一思想:集合$A_n = {a_1, \cdots , a_n}$的所有子集可以分成两组:不包含$a_n$ 的子集
和包含$a_n$的子集,前一组是 $A_{n-1}$的所有子集,而后一组中的每一个元素都可以
通过把 $a_n$添加到 $A_{n-1}$ 的所有子集中得到。
减常因子算法
折半查找
用于有序数组的查找
用递归方法很容易实现,非递归方法也可以:

效率: $O(logn)$
假币问题
问题定义:从$n$个硬币中找出一个假的硬币,假的硬币重量与真的硬币重量不同(假币更轻)。
1.把硬币分为两堆
2.把硬币分为三堆,那么期望称重的次数大约会是 $log_3n$
俄式乘法
问题定义:
如果$n$是偶数,那么:
$n \times m = (n/2) \times (2m)$
如果是奇数,那么:
$n \times m = (n-1)/2 \times (2m) + m$
停止条件: $1 \times m = m$
计算 $ 50 \times 65$ 的例子:

对于硬件来说执行速度很快。
约瑟夫斯问题
幸存者问题,$n$ 个人围成一个圈,编号为从1到$n$ ,从编号为1的人开始计数,每次消去第二个人
直到只留下一个幸存者。这个问题就是要求算出幸存者的号码 $J(n)$
n为偶数的时候,$J(2k) = 2J(k) -1$
n为奇数的时候,$J(2k + 1) = 2J(k) + 1$
初始条件,$J(1) = 1$
一种求解方法:应用前向替代法,求出$J(n)$的前几个值,找出一个模式,使用数学归纳法进行证明。
减可变规模算法
计算中值和选择问题
问题定义:选择问题是求一个$n$个数列表的第$k$个最小元素的问题,这个数字被称为第
$k$个顺序统计量,当$k = \lceil n/2 \rceil $ 时,就是找中值的问题了。

使用划分列表来寻找第 $k$ 个最小元素:

最差效率: $O(n^2)$
最好效率 : $O(n)$
插值查找
假设有序数组是线性递增的,
插值查找为了找到用来和查找键进行比较的数组元素,考虑了查找键的值。
效率分析表明:
在查找一个包含n个随机键的列表时,平均来说,插值查找的键值比较次数要小于 $log_2 log_2 n +1 $
插值查找和折半查找的对比:
对于较小的文件,折半查找可能更好,但对于更大的文件和那些比较的开销非常大或者访问的成本非常高的应用,
插值查找更值得考虑。
二叉查找树
定义:这种二叉树的节点包含了可排序项集合中的元素,并且对每个节点来说,
所有左子树的元素都小于子树根节点的元素,所有右子树的元素都大于子树根节点的元素。
查找一个给定值为 $v$ 的元素:
如果这颗树为空,则查找失败
否则将 $v$与输的根 $K(r)$ 进行比较,如果它们相等,则查找停止,
若 $ v < K(r) $ ,在左子树中继续查找
若$ v > K(r) $ ,在右子树中继续查找。
最差效率: $\Theta(n)$
平均效率: $\Theta(logn)$
Nim游戏
问题定义:有两个玩家轮流走,每个玩家有同样的可选走法,每种步数有限的走法都会形成
同样游戏的较小实例,最后以为能够移动的玩家就是胜者。
例子:有n个棋子,两个人轮流从其中拿走最少1个,最多m个棋子,每次拿走的棋子数可以不用,
但上下限数量不变,请问哪个问价能拿到最后的胜利,先走的还是后奏的,采取什么策略?
分析:
$n = 0$ :败局
$ 1 \leq n \leq m $ : 胜局
$ n = m+1 $ :败局,合法拿走任意数量的棋子都会把对方推入胜局
$ m+2 \leq n \leq 2m+2 $ : 胜局,走一步之后就可以留给对方 $ m + 1$ 个棋子
…
用数学归纳法可以证明,当且仅当 $n$ 不是 $m+1$ 的倍数时,$n$个棋子的实例是一个胜局。
胜利的策略是在每次拿走$ n mod (m+1) $ 个棋子,若背离这个策略,就会把胜局留给对手。