分治法
主定理
对于通用分治递推式: $T(n) = aT(n/b) + f(n)$
那么:

合并排序
对于一个需要排序的数组,合并排序将它一分为二,并对每个子数组递归排序,然后把这两个排好序的子数组
组合并为一个有序数组。

其中 $Merge$ 函数是将两个有序数据进行合并:

复杂度分析:
键值比较次数 $C(n)$
当 $n > 1$ 时, $C(n) = 2C(n/2) + C_{merge}(n) , C(1) = 0$
令 $ n = 2^k$ ,容易求得:
$C_{worst}(n) = nlog_2n - n + 1$
快速排序
快速排序按照元素的值对它们进行划分,建立了一个划分以后,$A[s]$ 已经位于它在有序数组中的最终位置,
接下来我们可以继续对 $A[s]$ 前和 $A[s]$后的子数组进行排序。

最优效率:
此时每次划分都可以恰好将数组分成大小相同的两部分,容易得到
当 $n>1$ 时, $C_{best}(n) = 2C_{best}(n/2) + n , C_{best}(1) = 0$
对于 $n = 2^k$ 的情况, $C_{best}(n) = nlog_2n$
最差的效率:
已经是严格递增的数组了,
$C_{worst}(n) \in \Theta(n^2)$
快速排序有一个重要的特点是,它的平均效率只比最优情况多执行39%的操作,
这使得它在实际中应用很广泛。
二叉树遍历及其相关特性
把二叉树定义为若干节点的一个有限集合,它要么为空,要么由一个根和两棵树称为
$T_L$ 和 $T_R$ 的不相交二叉树构成,这两科二叉树分别为根的左右子树。

除此之外,二叉树的遍历也蕴含这分治的思想,
前序遍历,中序遍历,后序遍历。
大整数乘法和 Strassen矩阵乘法
这两个算法都通过巧妙地运用分治技术来获得更好的渐进效率。
大整数乘法
应用:密码技术里面经常需要对超过100位的十进制整数进行乘法计算。
对于两个大整数 $a = a_1a_0 , b = b_1b_0$
其中 $a = a_110^{(n/2)} + a_0$
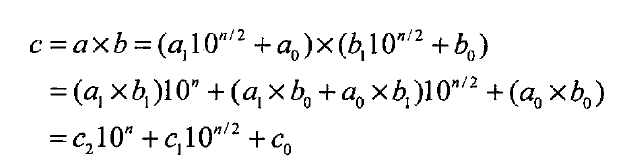
其中 $c_2 = a_1 \times b_1$
$c_0 = a_0 \times b_0$
$c_1 = (a_1 + a_0) \times (b_1 + b_0) - (c_2 + c_0)$
这样$n$位数的乘法需要对 $n/2$位数做三位乘法运算,乘法次数$M(n)$的递推式如下:
$n> 1 时, M(n) = 3M(n/2), M(1) = 1$
当$n = 2^k时, M(2^k) = 3^k$
所以$M(n) = 3^{log_2n} $
Strassen矩阵乘法
计算两个 $2 \times 2$矩阵乘积:

计算两个$n$个方阵时执行的乘法次数:
$n > 1, M(n) = 7M(n/2) , M(1) =1$
用分治法解最近对问题和凸包问题
解决最近对问题
$ 2 \leq n \leq 3 $: 使用 蛮力算法进行求解
$n > 3$ : 可以利用点集在 $x$ 轴方向上的中位数 $m$ ,在该处
做一条垂线,将点集分文两个子集,然后对两个子集分别求求解,
注意合并的时候,还应该考虑到最近的两个点可能分别位于分界线的两侧,
因此在合并较小子问题的解的时候,需要检查是否存在这样的点。


复杂度: $T(n) \in \Theta(nlogn)$
凸包问题
略