蛮力法
蛮力法(brute force)是一种简单直接地解决问题的方法,常常直接基于问题的描述和所涉及的概念定义。
选择排序和冒泡排序
选择排序:开始的时候,扫描整个列表,找到最小元素,然后和第一个元素交换,
然后从第二个元素开始扫描,找到最后$n-1$ 个元素中的最小元素,再和第二个元素交换位置,
把第二小的元素放在它的位置上,依次类推。
伪代码:

算法复杂度: $\Theta(n^2)$
键的交换次数: $\Theta(n)$
冒泡排序
比较表中的相邻元素,如果他们是逆序的话就交换他们的位置,
重复多次,最大的元素就到了最后一个位置,第二遍操作将第二大的元素沉下去,
$n-1$ 遍之后,该列表就排好序了。
复杂度: $\Theta(n^2)$
键交换次数和键比较次数: $\Theta(n^2)$

稳定性
如果一个排序算法保留了等值元素在输入中的相对顺序,就可以说它是稳定的。
顺序查找

简单地将给定列表中的连续元素和给定的查找键进行比较,直到遇到一个匹配的元素。
蛮力字符串匹配
从文本中寻找匹配模式的子串

最近对问题的蛮力算法
最近对问题要求在一个包含$n$个点的集合中,找出距离最近的两个点。
显然:分别计算每一对点之间的距离,然后找出距离最小的那一对。
为了避免对同一对点计算两次距离,只考虑 $i < j$ 的那些对 $(p_i, p_j)$

复杂度: $\Theta(n^2)$
凸包问题
凸集合 对于平面上的一个点集合(有限的或无限的),如果以集合中的任意两点 $p$ 和 $q$ 为端点的线段都属于该集合,我们说这个集合是 凸的。
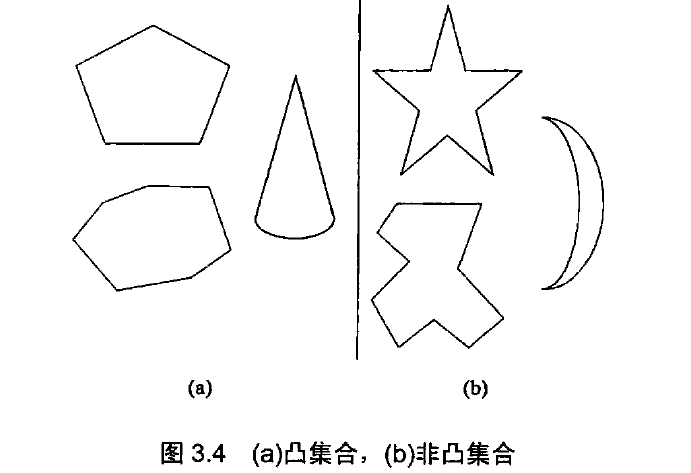
凸包: 对于平面上$n$ 个点的集合,它的凸包就是包含所有这些点(或者在内部,或者在边界上)的最小凸多边形。
很明显,任意包含 $n>2$个点的集合$S$的凸包是以$S$中的某些点为定点的凸多边形。这些定点称为极点。
凸包问题(convex-hull problem)是为一个有$n$个点的集合构造凸包的问题。
蛮力法的解决方式:对于一个$n$个点集合中的两个点$p_i$和 $p_j$ ,当且仅当该集合中的其他点都位于
穿过这两点的直线的同一边时,他们的连线是该集合凸包边界的一部分。对每一对点都做一遍检验之后,
满足条件的线段构成了该凸包的边界。
时间效率为$O(n^3)$, 对于每一对不同点对 $n(n-1)/2$来说,我们要对其他 $n-2$个点求出
他们是否满足都位于直线的同一边。
穷举查找
对于组合问题来说,穷举查找是一种简单的蛮力方法。它要求生成问题域中的每一个元素,选出其中满足问题约束的元素,然后再找出一个期望元素(例如,使目标函数达到最优的元素)。
旅行商问题(traveling salesman problem,TSP)
要求找出一条 $n$个给定的城市间的最短路径,使我们在回到出发的城市之前,对每个城市都只访问一次。
建模:用加权图,图的顶点表示城市,边的权重表示城市间的距离,这样问题就可以表述为求一个图的最短
哈密顿回路(Hamiltonian circuit)。
容易想出来,哈密顿回路也可以定义为 $n+1$个相邻顶点 的一个序列,其中,
第一个顶点和最后一个已经固定,
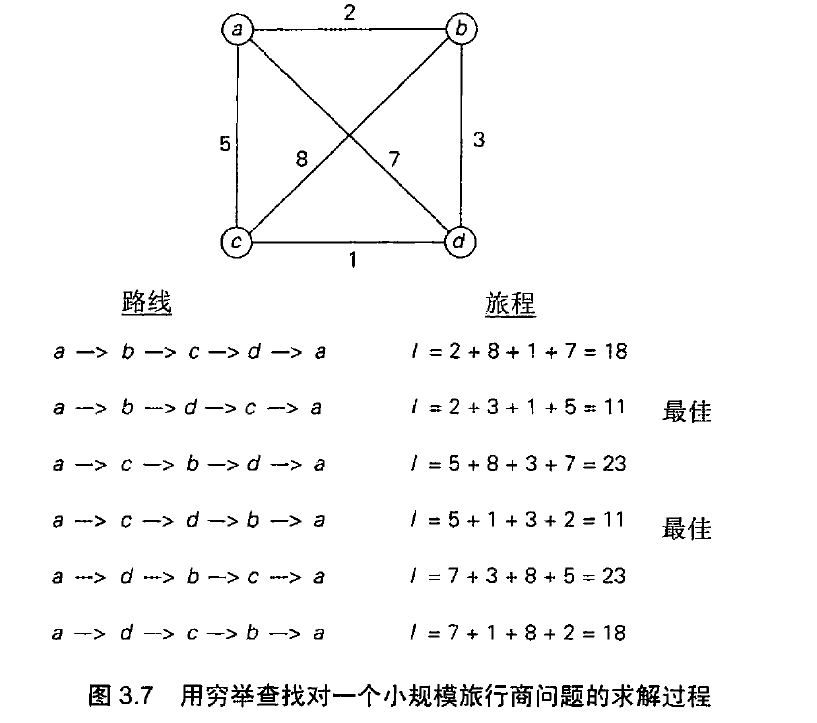
因此可以通过生成 $n-1$ 中间城市的组合来得到所有的旅行线路,计算这些线路的长度,然后求得最短
的线路。
复杂度: $O(n!)$
背包问题
定义: 给定$n$个重量为 $w_1, w_2, \cdots , w_n$,价值为 $v_1, v_2, \cdots, v_n$
的物品和一个承重为$W$ 的背包,求这些物品中一个最有价值的子集,并且要能够
装到背包中。
因为一个 $n$元素集合的子集数量是$2^n$,所以不论生成独立子集的效率有多高,
穷举查找都会导致一个 $\Omega(2^n)$的算法。
这两个问题(TSP,背包问题)就是所谓的 NP困难问题中最著名的例子,
对于NP困难问题,目前没有已知的效率可以用多项式来表示的算法。
回溯法和分支界限法使我们可以在优于指数级的效率下解决该问题的部分实例,
或者也可以使用近似算法。
分配问题
定义:有 $n$个任务需要分配给$n$个人执行,一个任务对应一个人,
对于每一对 $i,j = 1,2, \cdots, n$来说,将第$j$个任务分配给第$i$个任务的成本
是$C[i,j]$。 该问题是要找出总成本最小的分配方案。
建模:用一个成本矩阵$C$来表示,行代表人,列代表任务,值就是成本,这个问题相当于要求在矩阵的每一行中选出一个元素,这些元素分别属于不同的列,而且元素的和是最小的。
穷举查找:生成整数$1,2,3, \cdots, n$的全部排列,然后把成本矩阵中的相应元素相加来求得每种分配方案的总成本,最后选出其中具有最小和的方案。
效率: $O(n!)$
深度优先查找和广度优先查找
深度优先查找(depth-first search,DFS)
深度优先查找从任意顶点开始访问图,把该顶点标记为已访问,在每次迭代的时候,该算法紧接着处理与当前顶点领接的未访问顶点,一直持续,直到遇见一个终点,这个终点的所有领接顶点都被访问过了,于是,算法沿着来路后退一条边,并试着继续从那里访问未访问的顶点,持续这个过程,直到算法回到起始顶点,并且起始顶点也是一个终点。
伪代码:

一个例子:
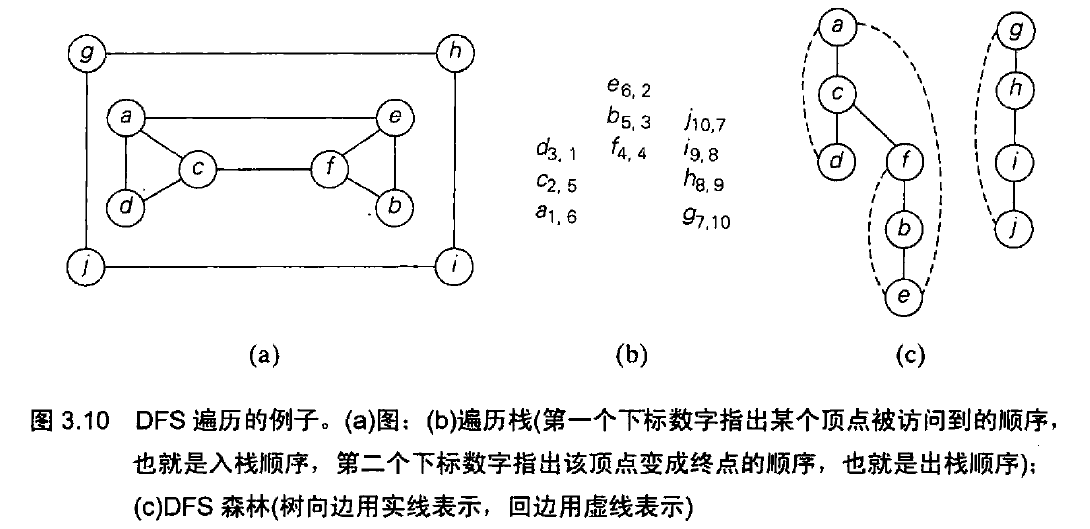
其中遍历栈是用来追踪深度优先查找的操作,在第一次访问一个顶点时,将该顶点入栈,当它成为一个终点时,我们把它出栈。
深度优先查找森林:初始顶点作为森林中的第一棵树的根,遇到一个未访问的顶点时,它是从哪个顶点被访问到的,就把它附加为哪个顶点的子女,连接这样两个顶点的边称为树向边(tree edge),当该算法遇到一条指向已访问的节点的时候,并且这个顶点不是它的直接前驱,我们把这种边称为回边(back edge)。
效率:
它消耗的时间和用来表示图的数据结构的规模是成正比的,
对于邻接矩阵表示法,该遍历的时间效率属于 $\Theta(|V|^2)$,
对于邻接链表表示法,它属于 $\Theta(|V| + |E|)$,
其中$|V|$和$|E|$分别是图的顶点和边的数量。
DFS重要的基本应用:
-
检查图的连通性:从任意一个节点开始DFS遍历,在该算法停下来之后,检查一下是否所有的顶点都被访问过了,如果都访问过了,那么这个图是连通的。
-
无环性。利用图的DFS森林形式的表示法,如果DFS森林不包括回边,这个图显然是无回路的。
广度优先查找(breadth-first search, BFS)
首先访问所有和初始顶点邻接的顶点,然后是离初始顶点两条边的所有未访问的顶点,依次类推。
使用队列跟踪广度优先查找的操作,首先从遍历的初始顶点开始,将该顶点标记为已访问,
每次迭代的时候,该算法找出所有和队头顶点邻接的未访问顶点,把它们标记为已访问,再把它们入队。
然后,将队头顶点从队列中移去。
广度优先查找森林: 初始顶点作为一个森林中第一棵树的根,无论何时,只要第一次遇到一个
新的未访问顶点,它是从哪个顶点被访问到的,就把它附加为哪个顶点的子女,连接这样的两个顶点
的边称为树向边(tree edge),若一条边指向曾经访问过的顶点,且该顶点不是它的直接前驱,
那么这种边称为交叉边。
伪代码

例子:
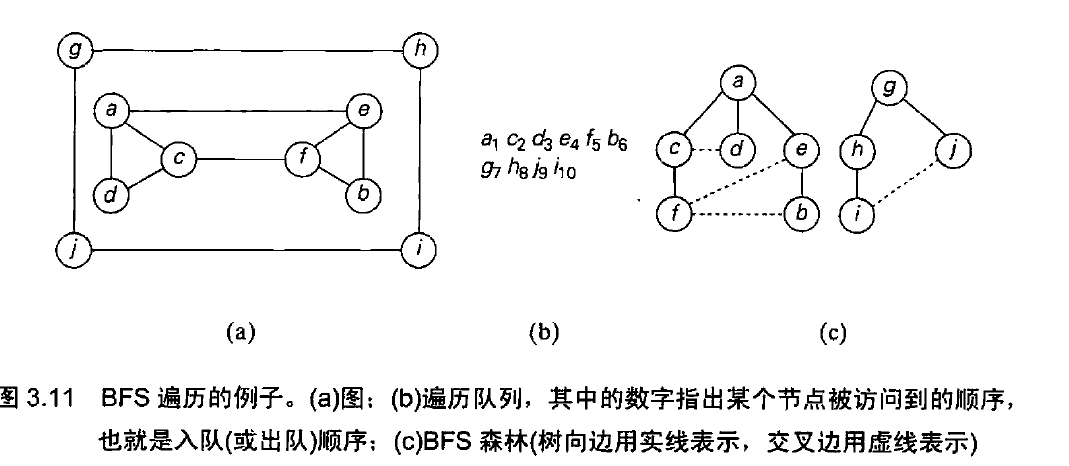
效率与DFS相同
应用:同样也能用来检查图的连通性和无环性,做法本质上和DFS相同。
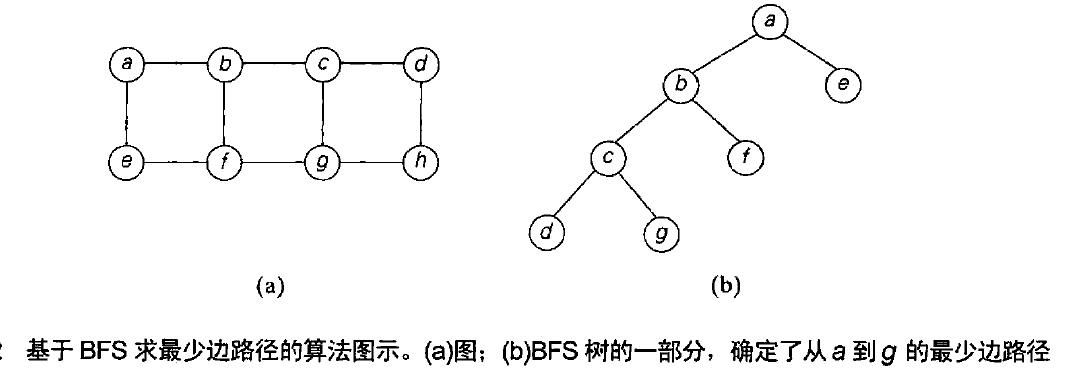
用来求两个给定顶点之间的数量最少的路径:从给定的一个顶点开始BFS,一旦访问到了另一个顶点就结束,
从BFS树的根到第二个顶点间的最简单路径就是我们求得的路径。
比较:
