本文目录

神经网络

神经网络

神经元模型

神经网络是具有适应性的简单单元组成的广泛并行互连的网络，它的组织能够模拟生物神经系统对真实世界物体所作出的交互反应。

—- Kohonen 1988

神经网络中最基本的成分是神经元（neuron）模型：

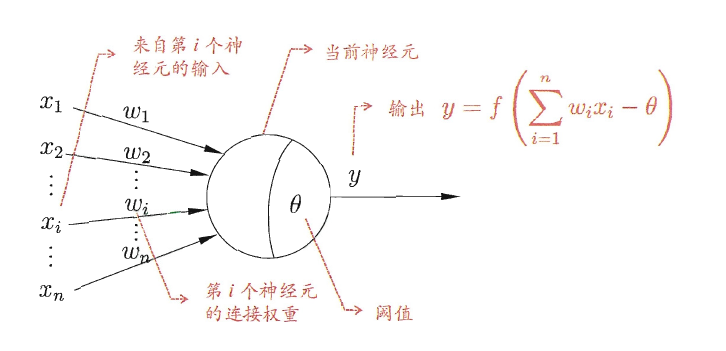
在这个模型中，神经元接收来自$n$个其他神经元传递过来的输入信号，这些输入信号通过带权重的连接进行传递，神经元接收到的总输入值将与神经元的阈值进行比较，然后通过激活函数处理以产生神经元的输出。

感知机和多层网络

感知机（Perceptron）由两层神经元组成：

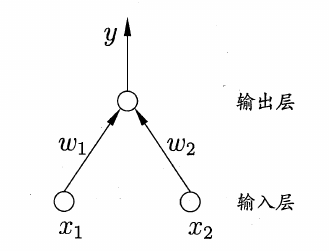
给定训练数据集，权重$w_i (j= 1,2, \cdots, n)$以及阈值$\theta$可通过学习得到。将阈值$\theta$看成是一个固定输入为-1.0的哑结点所对应的连接权重$w_{n+1}$，这样对训练样例$(x, y)$，若当前感知机的输出为$\hat y$，则感知机的权重将这样调整（采用误分类点到超平面的总距离作为损失函数，然后使用梯度下降法可得下面的公式）：

$\begin{array}{c}{w_{i} \leftarrow w_{i}+\Delta w_{i}} \\ {\Delta w_{i}=\eta(y-\hat{y}) x_{i}}\end{array}$

若训练数据集是线性可分的，那么感知机的学习过程一定会收敛，否则感知机的学习过程将会发生振荡，$w$难以稳定下来。

要解决非线性可分问题，需要使用多层功能神经元。下面是两个多层前馈神经网络的示意图：

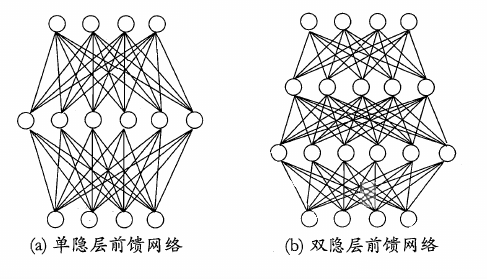
这里的“前馈”并不意味着网络中的信号不能像后传，而是指网络拓扑结构上不存在环或回路。

误差逆传播算法

误差逆传播（error BackPropagation，简称BP）算法是多层网络的学习算法。

BP算法基于梯度下降（gradient descent）策略，以目标的负梯度方向对参数进行调整。对每个训练样例，BP算法的工作流程如下：

先将输入示例提供给输入层神经元，然后逐层将信号前传，知道产生输出层的结果（前向传播）
计算输出层的误差，将误差逆向传播至隐层神经元，根据隐层神经元的误差来对连接权和阈值进行调整，该迭代过程循环进行，直到达到某些停止条件为止。

每次仅针对一个训练样例更新连接权和阈值，这样的BP算法称为标准BP算法，与之相对的，还可以在读取整个训练集一遍之后才对参数进行更新，此时的BP算法称为累积BP算法。

需要注意的是，如果误差函数具有多个局部最小，则不能保证找到的解是全局最小。以下是几种让模型训练“跳出局部最小”的策略：

以多组不同的参数值初始化多个神经网络，从多个不同的初始点开始搜索。
使用模拟退火技术，模拟退火技术每一步都以一定的概率接受比当前解更差的结果。
使用随机梯度下降（标准BP算法），随机梯度下降在计算梯度的时候加入了随机因素。

其中BP算法的数学原理可以参考百面机器学习9.3

神经网络的训练技巧

由于其强大的表示能力，BP神经网络在实际应用中经常遭遇过拟合，缓解过拟合的策略有两种：

早停，若训练集误差降低但验证集误差升高，则停止训练。
正则化，在误差目标函数中增加一个用于描述网络复杂度的部分。
模型集成等…

Dropout

其中Dropout是模型集成方法中最高效与常用的技巧。

Dropout的具体流程是，在训练中要求某个神经元节点激活值以一定的概率p被“丢弃”，即该神经元暂时停止工作。因此，对于包含N个神经元节点的网络，在Dropout的作用下可看作为$2^N$个模型的集成（类似于Bagging）。这$2^N$个模型可认为是原始网络的子网络，它们共享部分权值，并且具有相同的网络层数，而模型整体的参数数目不变，这就大大简化了运算。

Batch Normalization

随着网络训练的进行，每个隐层的参数变化使得后一层的输入发生变化，从而每一批训练数据的分布也随之改变，致使网络在每次迭代中都需要拟合不同的数据分布，增大训练的复杂度以及过拟合的风险。

批量归一化方法是针对每一批数据，在网络的每一层输入之前增加归一化处理$($均值为0，标准差为1$)$，将所有批数据强制在统一的数据分布下，从而增强了模型的泛化能力。但是批量归一化同时也降低了模型的拟合能力，为了恢复原始数据分布,具体实现中引入了变换重构以及可学习参数$\gamma$和$\beta$ 。

完整的批量归一化网络层的前向传导过程公式如下：

$\begin{array}{c}{\mu_{\mathcal{B}} \leftarrow \frac{1}{m} \sum_{i=1}^{m} x_{i}} \\ {\sigma_{\mathcal{B}}^{2} \leftarrow \frac{1}{m} \sum_{i=1}^{m}\left(x_{i}-\mu_{\mathcal{B}}\right)^{2}} \\ {\hat{x}_{i} \leftarrow \frac{x_{i}-\mu_{B}}{\sqrt{\sigma_{B}^{2}+\epsilon}}} \\ {y_{i} \leftarrow \gamma \hat{x}_{i}+\beta \equiv B N_{\gamma, \beta}\left(x_{i}\right)}\end{array}$

使用批量归一化的好处：

1.加快训练速度，使深层神经网络更容易训练

a.可以使用更大的学习速率

b.有效减少梯度消失或者爆炸的问题

2.学习过程可以更少的受参数初始化的影响

3.提高模型的泛化能力

常用激活函数

线性模型是机器学习领域中最基本也是最重要的工具，以逻辑回归和线性回归为例，无论通过闭解形式还是使用凸优化，它们都能高效且可靠地拟合数据。然而真实情况中，我们往往会遇到线性不可分问题$($如XOR异或函数$)$，需要非线性变换对数据的分布进行重新映射。对于深度神经网络，我们在每一层线性变换后叠加一个非线性激活函数，以避免多层网络等效于单层线性函数，从而获得更强大的学习与拟合能力。

Sigmoid激活函数

Sigmoid激活函数的形式为：

$f(z)=\frac{1}{1+\exp (-z)}$

对应的导函数为：

$f^{\prime}(z)=f(z)(1-f(z))$

图像如下所示：

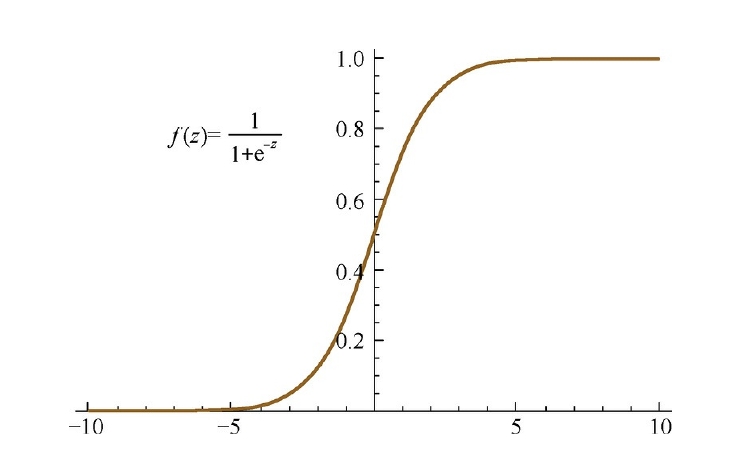
Tanh激活函数

Tanh激活函数的形式为

$f(z)=\tanh (z)=\frac{\mathrm{e}^{z}-\mathrm{e}^{-z}}{\mathrm{e}^{z}+\mathrm{e}^{-z}}$

对应的导函数为

$f^{\prime}(z)=1-(f(z))^{2}$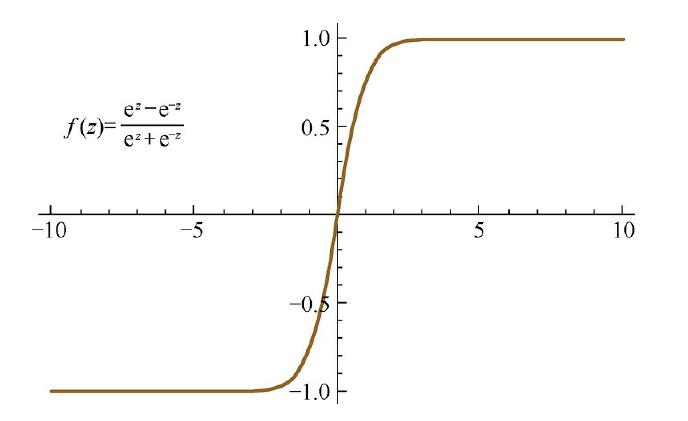

ReLU激活函数

ReLU激活函数的形式为：

$f(z)=\max (0, z)$

对应的导函数为：

$f^{\prime}(z)=\left\{\begin{array}{l}{1, z>0} \\ {0, z \leqslant 0}\end{array}\right.$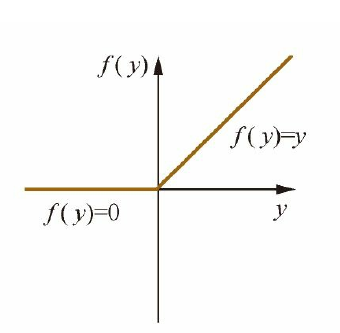

三者的比较

由Sigmoid以及Tanh的图像容易知道，当$z$很大或者很小的时候，其导数$f^\prime(z)$都会趋近于0，即出现“梯度消失”的情况，实际上Tanh激活函数在数学上等于Sigmoid的平移：

$\tanh (x)=2 \operatorname{sigmoid}(2 x)-1$

相比之下，ReLU的非饱和性可以有效地解决梯度消失的问题，提供相对宽的激活边界。

从计算的角度上来说，Sigmoid和Tanh激活函数均需要计算指数，复杂度高，而ReLU只需要一个阈值即可得到激活值。
ReLU的单侧抑制提供了网络的稀疏表达能力。（稀疏表达约束深度网络大部分神经元节点处于抑制状态，即输出值为0；只有少数神经元处于活跃状态，输出值非0。）

ReLU也存在一定的局限性：其训练过程中会导致神经元死亡的问题。这是由于函数导致负梯度（包含参数更新的方向信息）在经过该ReLU单元时被置为0，且在之后也不被任何数据激活，即流经该神经元的梯度永远为0，不对任何数据产生响应。在实际训练中，如果学习率(Learning Rate)设置较大，会导致超过一定比例的神经元不可逆死亡，进而参数梯度无法更新，整个训练过程失败。

为了解决这一问题，人们设计了Leaky ReLU(LReLU)，其形式表示为：

$f(z)=\left\{\begin{array}{cl}{z,} & {z>0} \\ {a z,} & {z \leqslant 0}\end{array}\right.$

一般a为一个很小的正常数。

常见问题

神经网络训练时是否可以将全部参数初始化为0?

对于一个全连接的深度神经网络，由于其同一层的任意神经元都是同构的，它们拥有相同的输入和输出，如果将参数全部初始化为同样的值，那么前向传播以及反向传播的取值都是完全相同的，学习过程将永远无法打破这种对称性，最终统一网络层的各个参数仍然是相同的。

所以我们需要随机地初始化神经网络参数的值。

参考

神经网络基础