本文目录
注意力机制
根据通用近似定理,前馈网络和循环网络都有很强的能力。但由于优化算法和计算能力的限制,在实践中很难达到通用近似的能力。特别是在处理复杂任务时,比如需要处理大量的输入信息或者复杂的计算流程时,目前计算机的计算能力依然是限制神经网络发展的瓶颈。
注意力作为一种人类不可或缺的复杂认知功能,指人可以在关注一些信息的同时忽略另一些信息的选择能力。当用神经网络来处理大量的输入信息时,也可以借鉴人脑的注意力机制,只选择一些关键的信息输入进行处理,来提高神经网络处理信息的能力。
分类
按照认知神经学中的注意力,可以总体上分为两类:
- 聚焦式(focus)注意力 :自上而下的有意识的注意力,称为聚焦式(Focus)注意力。聚焦式注意力是指有预定目的、依赖任务的、主动有意识地聚焦于某一对象的注意力。
- 显著性(Saliency-Based)注意力 : 自下而上的无意识的注意力,这种注意力是由外界刺激驱动的注意,不需要主动干预,也和任务无关。可以将max-pooling和门控(gating)机制来近似地看作是自下而上的基于显著性的注意力机制。
在人工神经网络中,注意力机制一般就特指聚焦式注意力。
计算流程
Attention函数的本质可以被描述为一个查询(query)到一系列(键key-值value)对的映射,如下图所示:
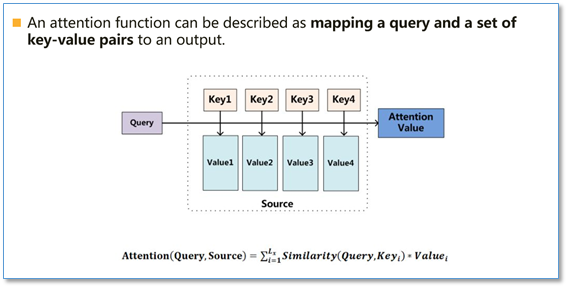
在计算attention时主要分为三步:
- 第一步是将query和每个key进行相似度计算得到权重,常用的相似度函数有点积,拼接,感知机,缩放点积等等;
- 第二步一般是使用一个softmax函数对这些权重进行归一化;
- 最后将权重和相应的键值value进行加权求和得到最后的attention。
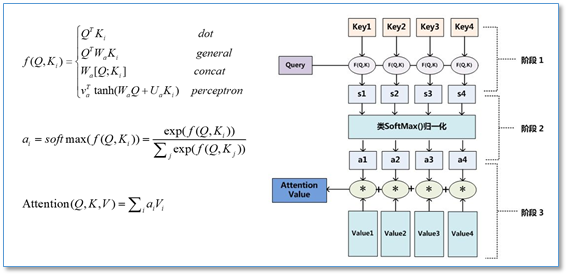
目前在NLP研究中,key和value常常都是同一个,即key=value。
上述编码方式为软性注意力机制(soft Attention): $Attention (Q, K, V)=\sum a_{i} V_{i}$ ,是实际应用中最常使用的方式。除了软性注意力机制,Attention机制还有下面这些变种:
-
硬性注意力(hard attention), 只关注到某一个位置上的信息。它的实现方式有两种,一种是选取最高概率的输入信息;另一种硬性注意力可以通过在注意力分布式上随机采样的方式实现。缺点是基于最大采样或随机采样的方式来选择信息。因此最终的损失函数与注意力分布之间的函数关系不可导,因此无法使用在反向传播算法进行训练。为了使用反向传播算法,一般使用软性注意力来代替硬性注意力。硬性注意力需要通过强化学习来进行训练。
-
键值对注意力, 此时key 与value不相等。
-
多头注意力:多头注意力(multi-head attention)的结构如下所示
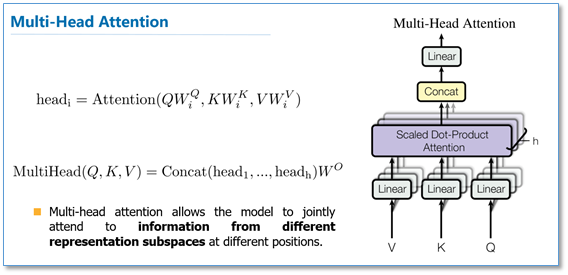
其中,Query,Key,Value首先进过一个线性变换,然后输入到放缩点积attention,注意这里要做h次,其实也就是所谓的多头,每一次算一个头。而且每次Q,K,V进行线性变换的参数W是不一样的。然后将h次的放缩点积attention结果进行拼接,再进行一次线性变换得到的值作为多attention的结果。多头attention的不同之处在于,它将一个查询分为h部分,进行了h次计算而不仅仅算一次,这样做的好处是允许模型在不同的表示子空间里学习到相关的信息,可以理解成让多个注意力关注输入信息的不同部分。多头注意力的数学表达如下:
- 结构化注意力,如果输入信息本身具有层次(hierarchical)结构,比如文本可以分为词、句子、段落、篇章等不同粒度的层次,我们可以使用层次化的注意力来进行更好的信息选择。此外,还可以假设注意力为上下文相关的二项分布,用一种图模型来构建更复杂的结构化注意力分布。
应用
指针网络
注意力机制计算过程中会产生一个注意力分布,这个分布表示输入信息的重要性程度。我们可以利用这个分布,将该分布作为一个软性的指针(pointer)来指出相关信息的位置。
指针网络(Pointer Network)是一种序列到序列模型,输入是长度为$n$ 的向量序列$X = x_1 , · · · , x_n $, 输出是下标序列$c_{1:m} = c_1 , c_2 , · · · , c_m ,c_i ∈ [1, n], ∀i$ 。指针网络在计算每一步解码的时候,会用到每个输入向量的注意力分布。具体的计算过程就不展开了,这里不做重点介绍,想看的话可以参考原论文或者神经网络与深度学习。
自注意力模型
当使用神经网络来处理一个变长的向量序列时,我们通常可以使用卷积网络或循环网络进行编码来得到一个相同长度的输出向量序列,基于卷积或循环网络的序列编码都是可以看做是一种局部的编码方式,只建模了输入信息的局部依赖关系(提取类似N-gram的特征)。虽然循环网络理论上可以建立长距离依赖关系,但是由于信息传递的容量以及梯度消失问题,实际上也只能建立短距离依赖关系。
如果要建立输入序列之间的长距离依赖关系,可以使用以下两种方法:一种方法是增加网络的层数,通过一个深层网络来获取远距离的信息交互;另一种方法是使用全连接网络。全连接网络是一种非常直接的建模远距离依赖的模型,但是无法处理变长的输入序列。
这时自注意力机制就派上用场了,它能够利用注意力机制的原理“动态”地生成不同连接的权重。
假设输入序列\(X=\left[\mathbf{x}_{1}, \cdots, \mathbf{x}_{N}\right] \in \mathbb{R}^{d_{1} \times N}\), 输出序列\(H=\left[\mathbf{h}_{1}, \cdots, \mathbf{h}_{N}\right] \in\mathbb{R}^{d_{2} \times N}\) ,我们先通过线性变换得到查询向量序列$Q$,键向量序列$K$以及值向量序列$V$:
\[\begin{aligned} Q &=W_{Q} X \in \mathbb{R}^{d_{3} \times N} \\ K &=W_{K} X \in \mathbb{R}^{d_{3} \times N} \\ V &=W_{V} X \in \mathbb{R}^{d_{2} \times N} \end{aligned}\]进一步地,由注意力机制的计算过程可以得到输出向量$h_i$:
\[\begin{aligned} \mathbf{h}_{i} &=\operatorname{att}\left((K, V), \mathbf{q}_{i}\right) \\ &=\sum_{j=1}^{N} \alpha_{i j} \mathbf{v}_{j} \\ &=\sum_{j=1}^{N} \operatorname{softmax}\left(s\left(\mathbf{k}_{j}, \mathbf{q}_{i}\right)\right) \mathbf{v}_{j} \end{aligned}\]如果使用缩放点积来作为注意力打分函数,输出向量序列可以写成:
\[H=V \operatorname{softmax}\left(\frac{K^{\mathrm{T}} Q}{\sqrt{d_{3}}}\right)\]其中softmax函数按列进行归一化。
自注意力模型与全连接模型的对比如下:
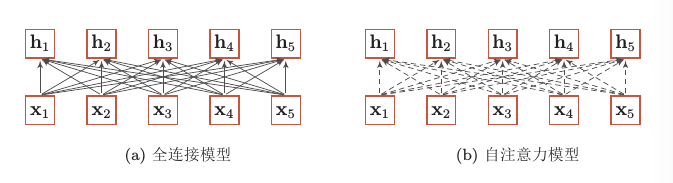
图中,实线表示可学习的权重,虚线表示动态生成的权重。自注意力模型的权重是动态生成的,其中$W_Q \in \mathbb{R}^{d_{3} \times d_{1}} , W_K \in \mathbb{R}^{d_{3} \times d_{1}}, W_V \in \mathbb{R}^{d_{2} \times d_{1}}$与输入的长度无关,因此可以处理变长的信息序列。
需要注意的是,自注意力模型计算的权重 $\alpha_{ij}$只依赖$q_i $和 $k_j$ 的相关性,而忽略了输入信息的位置信息。
假如我们将K、V按行进行打乱,那么Attention之后的结果是一样的(由上图也可以看出来)。但是序列信息非常重要,代表着全局的结构,因此必须将序列的分词相对或者绝对position信息利用起来。所以在单独使用时,自注意力模型一般需要加入位置编码信息来进行修正。
Transformer
Transformer的核心就是Attention机制,它的总体架构如下:
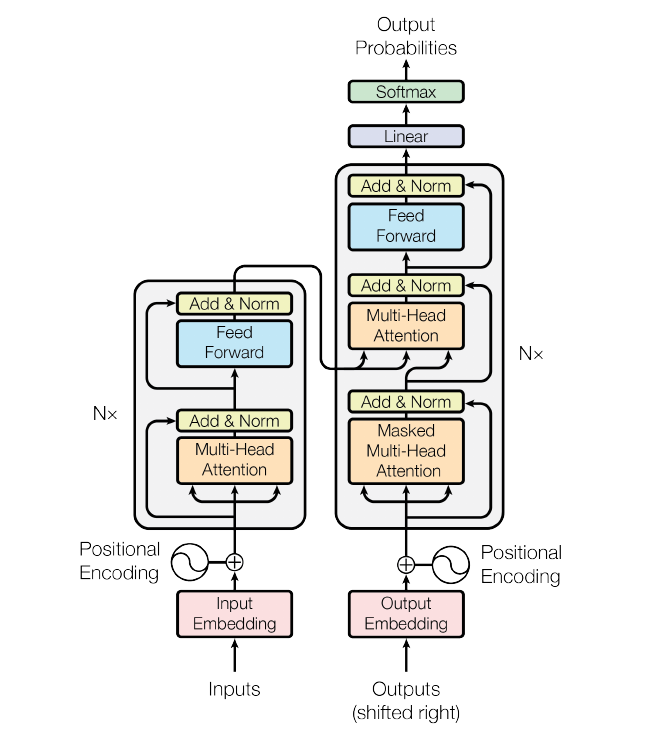
实际上它是一个Seq2Seq的模型,左边是encoder,对输入进行编码,右边是decoder,对编码后的特征进行解码。注意,左边encoder的输出,会和右边每一层的decoder进行结合:
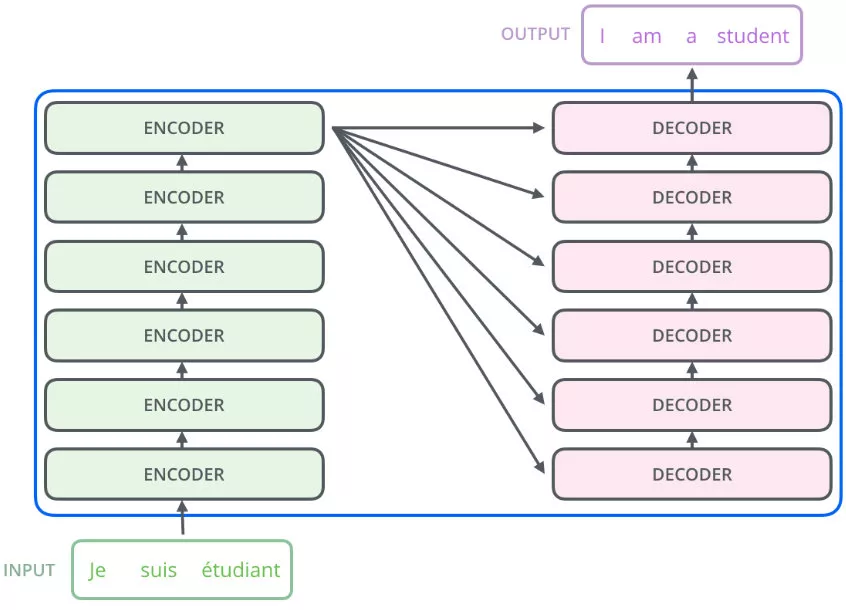
transformer的encoder有6层,每层包括2个sub-layers:
- 第一个sub-layer是multi-head self-attention mechanism,用来计算输入的self-attention
- 第二个sub-layer是Position-wise Feed-forward Networks, 简单的全连接网络,对每个position的向量分别进行相同的操作,包括两个线性变换和一个ReLU激活输出
在每个sub-layer都模拟了残差网络,每个\(c_{1:m} = c_1 , c_2 , · · · , c_m ,c_i ∈ [1, n]\), 任意isub-layer的输出都是$LayerNorm(x+Sublayer (x))$
单层Encoder的架构如下:
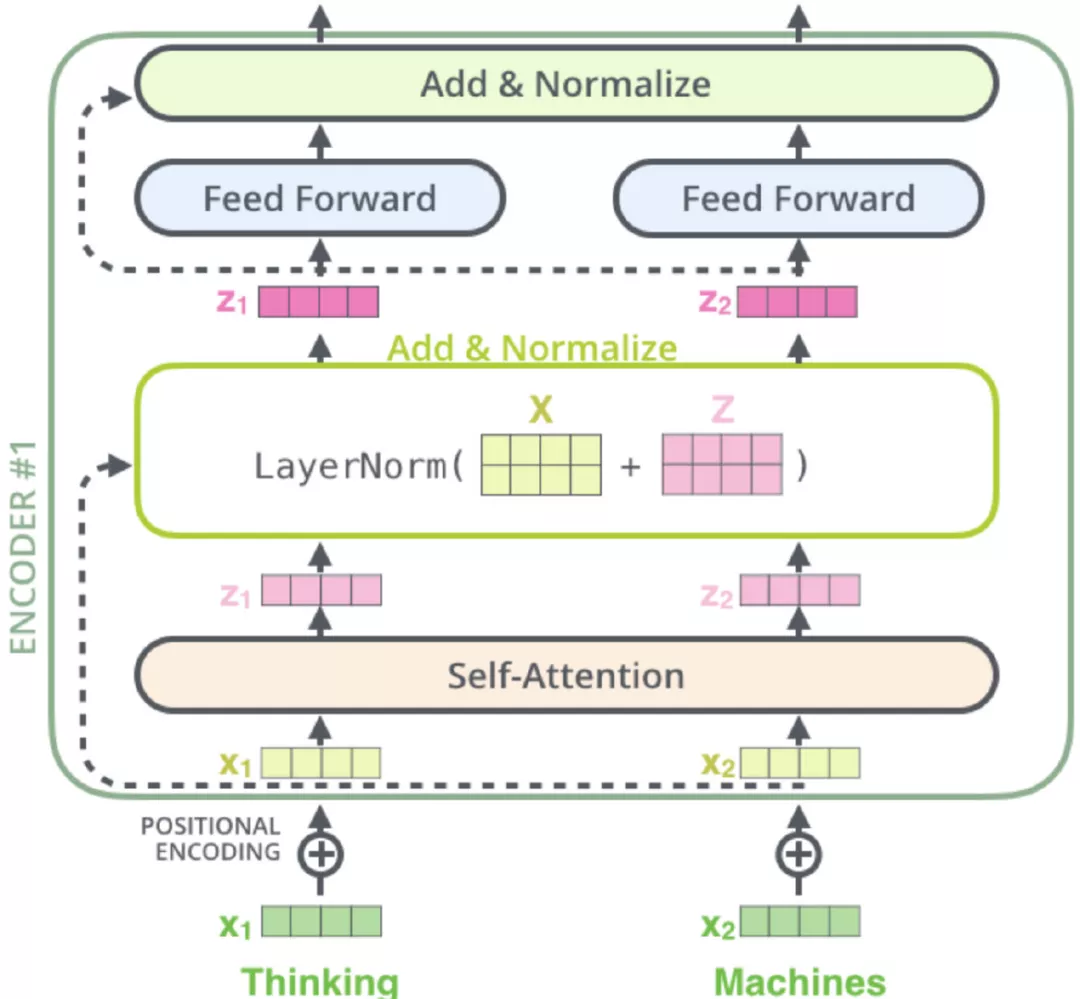
transformer的decoder也是6层,其中每层包括3个sub-layers:
- 第一个是Masked multi-head self-attention,也是计算输入的self-attention,但是因为是生成过程,因此在时刻 i 的时候,大于 i 的时刻都没有结果,只有小于 i 的时刻有结果,因此需要做Mask
- 第二个sub-layer是全连接网络,与Encoder相同
- 第三个sub-layer是对encoder的输入进行attention计算。同时Decoder中的self-attention层需要进行修改,因为只能获取到当前时刻之前的输入,因此只对时刻 t 之前的时刻输入进行attention计算,这也称为Mask操作。
decoder的架构如下图右下部分所示:
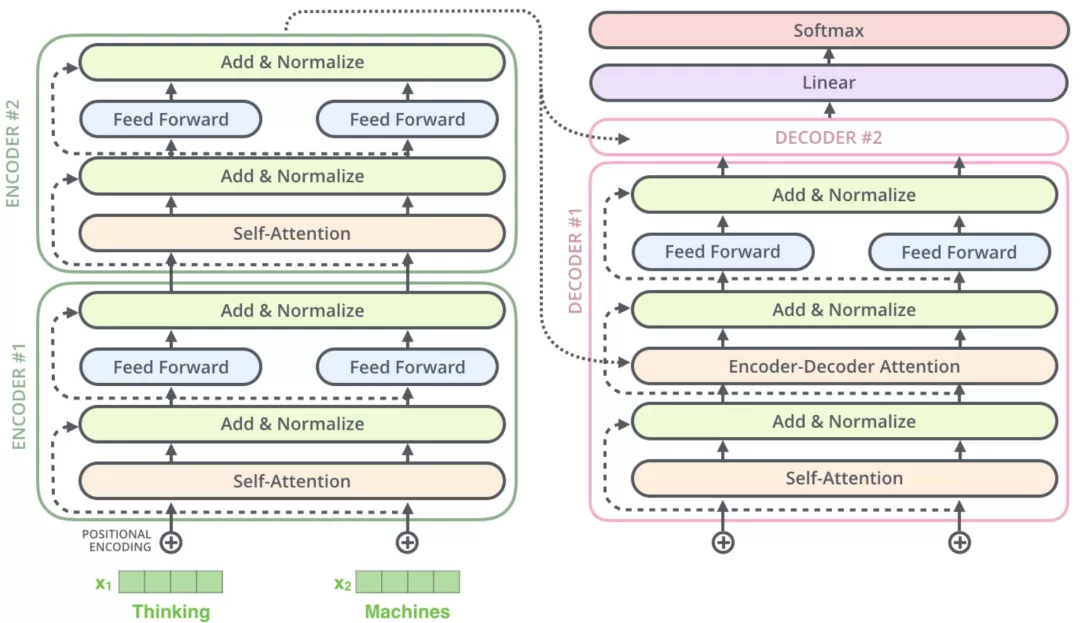
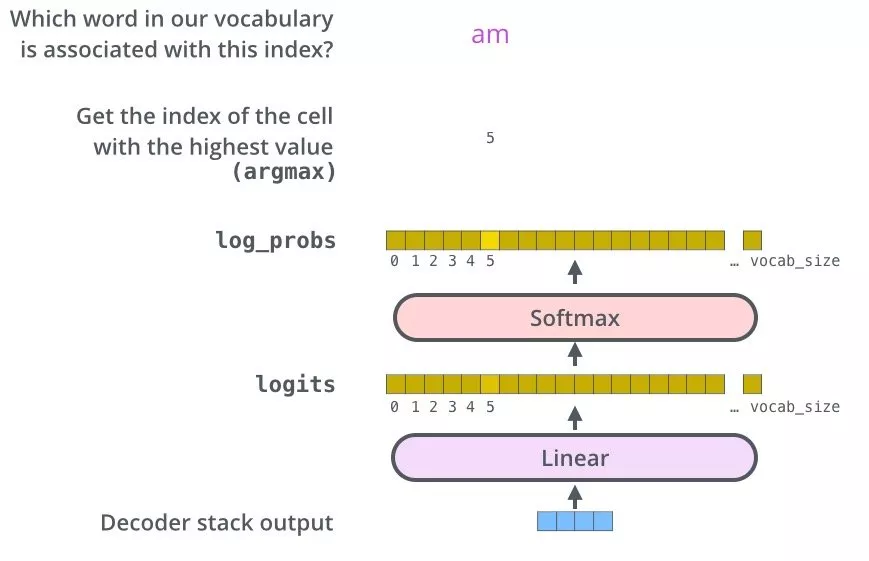
transformer的最后一层是将docoder的最后一层的输出作为输入,接一个线性层,再经过softmax归一化进行word预测:
需要重点注意的是,Transformer中的Attention机制由Scaled Dot-Product Attention和Multi-Head Attention组成:
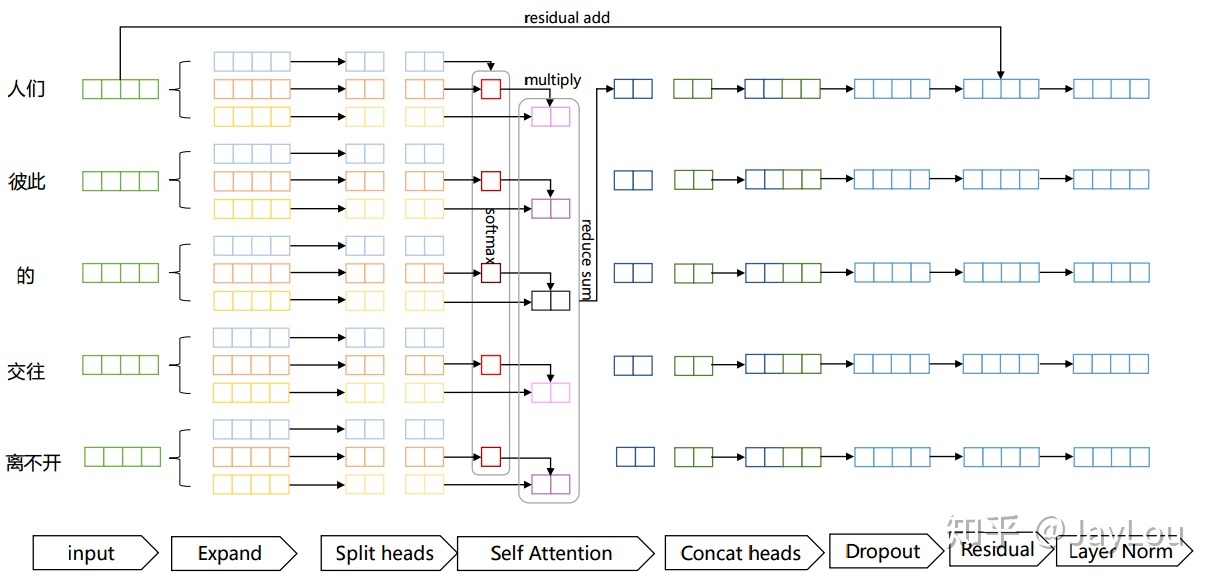
各个环节的解释如下:
- Expand:实际上是经过线性变换,生成Q、K、V三个向量;
- Split heads: 进行分头操作,在原文中将原来每个位置512维度分成8个head,每个head维度变为64;
- Self Attention:对每个head进行Self Attention,具体过程和第一部分介绍的一致;
- Concat heads:对进行完Self Attention每个head进行拼接;
公式为:
\[MultiHead(Q, K, V) = Concat(head_1, \cdots, head_h)W^O \\ 其中 head_i = Attention(QW_i^Q, KW_i^K, VW_i^V)\]参考
nlp中的Attention注意力机制+Transformer详解