变治法
变治法(transform-and-conquer),将问题分解成两个阶段工作:
”变“的阶段,把问题的实例变得更容易求解,
”治“的阶段,对实例进行求解。
变治思想有三种主要的类型:
- 变换为同样问题的一个更简单或者更方便的实例,实例化简。
- 变换为同样实例的不同表现,称为 改变表现。
- 变换为另一个问题的实例,这种问题的算法是已知的,称为问题化简。
下面是一些利用变治法解决问题的例子:
预排序
如果列表是有序的,许多关于列表的问题更容易求解。
比如:
-
检查数组中元素的唯一性,本来需要 $O(n^2)$ ,如果先使用合并排序对其进行排序,然后只检查它是否有
连续元素即可,这样的复杂度是 $O(nlogn)$
-
模式计算:找出给定数字列表中最常出现的一个数值
-
查找问题: 在给定数组中查找某个给定值$v$的问题
许多处理点集合的几何算法都使用了这样或那样的预排序,大多数基于贪婪技术的算法也都要求对其输入进行预排序。
高斯消去法
高斯消去法,就是将线性方程组用矩阵的方式来求解:

- 这里使用部分选主元法(partial pivoting),保证比例因子不会大于1,不会产生两个数量级相差非常大的数相减的情况。
- 计算temp使得过程更加高效。
时间复杂度 $O(n^3)$
LU分解
L矩阵:它是主对角线上的 “1”以及在高斯消去过程中行的乘数所构成的,
U矩阵:上三角矩阵则是消去的结果
一旦我们得到了矩阵$A$的LU分解,无论对于什么右边向量 $\mathbf{b}$ ,我们都可以对方程组 $\mathbf{A}x = \mathbf{b}$求解。
计算矩阵的逆
根据逆矩阵的定义,求出A的逆矩阵:即求出$n^2$个 $x_{ij}$ ,使得:
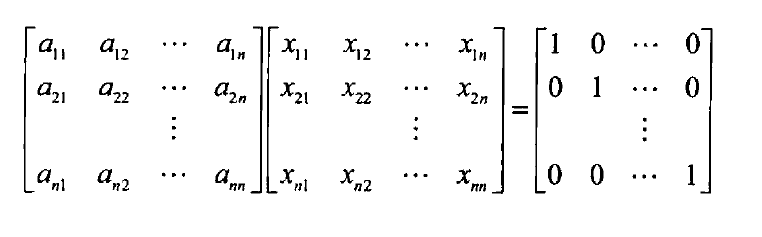
我们可以通过解$n$个具有相同系数矩阵$A$ 的线性方程组来求出这些未知数。这样就将计算矩阵的逆的问题转化为利用LU分解解线性方程的问题了。
### 计算矩阵的行列式
行列式的定义:
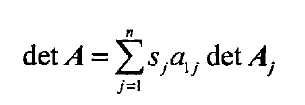
其中 $j$ 为奇数,$s_j = +1$,如果 $j$ 为偶数,$s_j = -1$,$a_{1j}$ 是位于1行$j$列的元素,
$\mathbf{A}_j$ 是一个$n-1$阶方阵,它是从矩阵 $\mathbf{A}$ 中删去了第一行和第$j$ 列后得到的。
行列式的定义是递归性的,使用递归定义来计算的话,复杂度为$O(n!)$。实际上,可以先用高斯消去法将矩阵化简为上三角的形式,那么行列式就等于对角线上的元素的乘积了。
平衡查找树
平衡查找树是对二叉查找树的改进,防止二叉查找树退化成严重不平衡的树。
两种方法:
- 实例化简,把一棵不平衡的二叉查找树转变成平衡的形式(自平衡的)。例子:AVL树要求它的每个节点的左右子树的高度差不能超过1,一棵红黑树能够容忍同一节点的一棵子树的高度是另一棵子树的两倍。如果一个节点的插入和删除违背了这些要求,就从一系列称为旋转的特定变换汇总选择一种,重新构造这颗树。
- 允许一棵查找树的单个节点不止包含一个元素,比如2-3树,2-3-4树,B树。
AVL树
定义:就是一棵二叉查找树,并且要求其中每个节点的左子树和右子树的高度差不能超过1。
AVL树通过旋转来保持平衡:
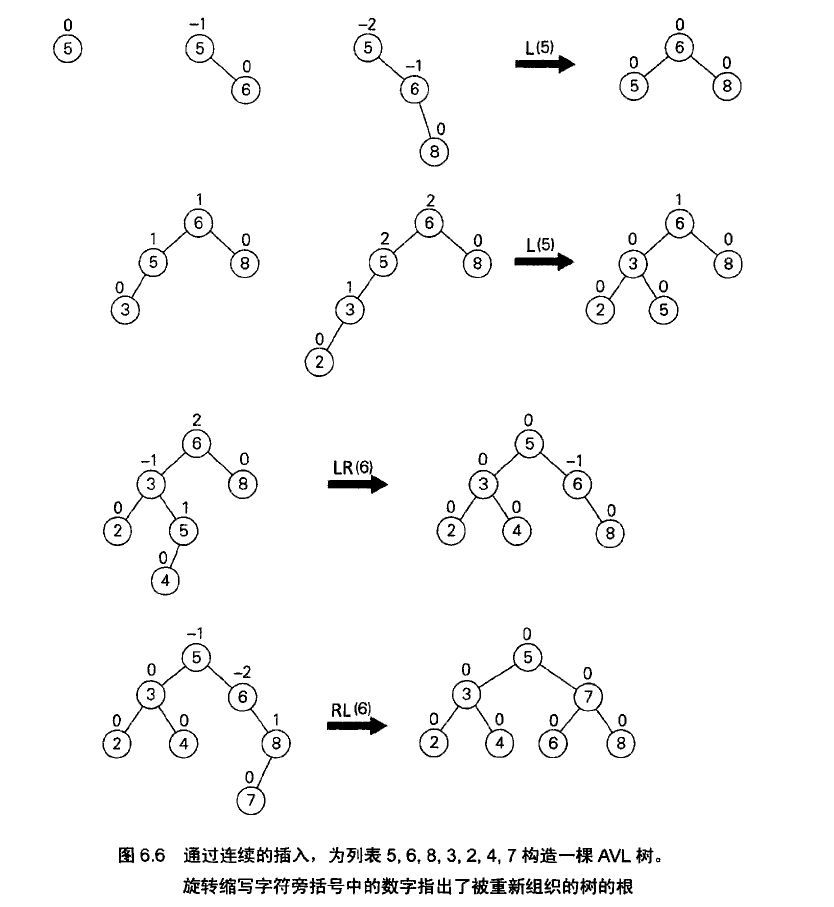
效率分析:
查找和插入和删除的操作效率都为 $\Theta(logn)$
但缺点是频繁的旋转,需要维护树的节点的平衡以及总体上的复杂性。
这些缺点阻碍AVL树成为实现字典(数组)的标准结构。
2-3树
2-3树是一种可以包含两种类型节点的树:2节点和3节点。
2节点只包含一个键$K$ 和两个子女:左子女作为一棵所有键都小于$K$ 的子树的根,
而右子女作为一棵所有键都大于$K$的子树的根。三节点包含两个有序的键 $K_1 K_2$
并且有三个子女,最左边的子女作为键值小于$K_1$ 的子树的根,中间的子女作为键值位于
$K_1 K_2 $ 之间的子树的根,最右边的子女作为键值大于$K_2$的子树的根。
最后一个要求:树中的所有叶子必须位于同一层。2-3树的具体形式可以参见下图:
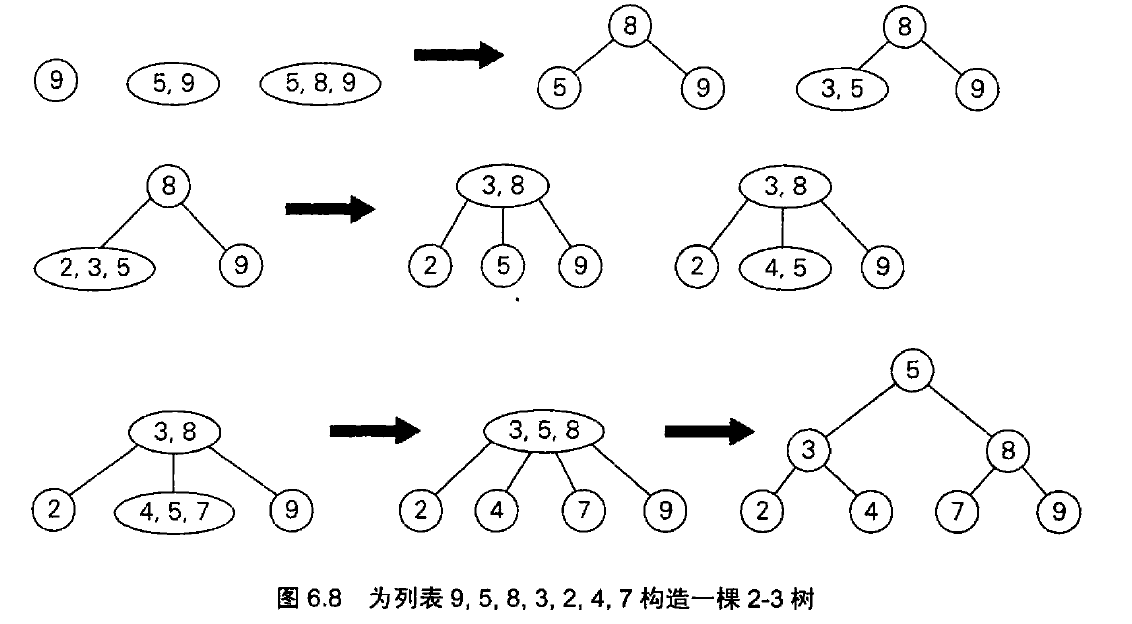
效率:通过对树的高度的分析,可知
无论在最差情况还是在平均情况,查找、插入、和删除的时间效率都属于$\Theta(log n)$
2-3树有一种重要的一般性的形式,就是B树。
堆和堆排序
堆的概念
定义 : 堆(heap)可以定义为一棵二叉树,树的节点中包含键(每个节点一个键),并且满足下面两个条件:
- 这棵二叉树是基本完备的(完全二叉树),就是说,树的每一层都是满的,除了最后一层最右边的元素有可能缺位
- 每一个节点的键都要大于或等于它子女的键
堆的特性:

针对一个给定列表,构造堆:
1.自底而上堆构造:先初始化一棵完全二叉树,然后从最后的父母节点开始,到根为止,检查这些节点的键是否满足父母优势要求,不满足则把节点的键K与它子女的最大键进行交换,然后再检查新位置上,K是不是满足父母优势要求,重复这个过程。

最差效率分析:每个位于树的第$i$层的键都会移动到叶子层$h$中
此时时间复杂度为 $O(n)$
2.另一种算法:通过把新的键连续插入预先构造好的堆,来构造一个新堆,自顶而下堆构造。
首先,把包含键K的新节点附加在当前堆的最后一个叶子后面,然后按照以下方法把K筛选到适当位置:
拿K和它父母的键作比较,后者大于等于K,算法停止,否则交换这两个键并把K和它的新父母做比较,
直到K不大于它的最后一个父母,或者称为根节点。
插入效率 $O(logn)$
堆排序
两个阶段:
- 构造堆,即为一个给定的数组构造一个堆(效率$O(n)$ )
- 删除最大键,即对剩下的堆应用$n-1$次根删除操作(效率$O(nlogn)$)
一般来说,堆排序比快速排序运行的慢,但和合并排序相比还是有竞争力的。
霍纳法则和二进制幂
问题:已知$x$ ,求多项式
$p(x) = a_nx^n + a_{n-1}x^{n-1} + \cdots + a_1x + a_0$
的值的问题,以及计算 $x^n$
霍纳法则
这是一个很好转化问题的例子。
对于上面讲的多项式,可以变形为
$p(x) = (\cdots (a_nx + a_{n-1})x + \cdots)x + a_0$
利用该变形可以写出伪代码:

它的乘法次数和加法次数都为 $n$
除此之外,该算法在计算 $p(x)$ 在某些点$x_0$上的值所产生的中间数字,恰好可以作为
$p(x)$除以$x - x_0$的商的系数,而算法的最后结果,除了等于 $p(x_0)$, 还等于这个除法的
余数。
二进制幂
用于计算 $a^n$的从左至右二进制幂:


效率:$O(logn)$ $n$为指数
比起蛮力法改善很多,蛮力法总是需要$n-1$次乘法
其他
除了上面列举的例子,还有一些基于问题化简策略的实例:
求最小公倍数
可以通过计算最大公约数来求得
因为最小公倍数和最大公约数存在以下关系:
$lcm(m,n) = \frac{m \times n}{gcd(m,n)}$
其中求最大公约数使用欧几里得算法很快。
计算图中的路径数量
用数学归纳法可以证明,从图中第$i$ 个顶点到第$j$个顶点之间,长度为$k>0$的不同路径的数量
等于$\mathbf{A}^k$ 的第$(i, j)$ 个元素,其中$\mathbf{A}$ 是这个图的邻接矩阵。
优化问题的化简
最大化问题和最小化问题可以相互化简
函数的最优化可以转化为求导数的问题
线性规划
许多决策最优化的问题都可以化简为线性规划问题的一个实例
线性规划问题是一个多变量线性函数的最优化问题。
一个解决这个问题的经典算法:单纯形法
这个算法的最差效率虽然是指数级的,但它在典型输入时的性能非常好
如果线性规划问题中的变量必须是整数,那么说这个线性规划问题是一个整数线性规划(Integer Linear programming)问题,对于一个一般的整数线性规划问题的任意实例来说,目前还没有一个已知的多项式
级的求解算法。
可以将背包问题转化为整数线性规划问题:
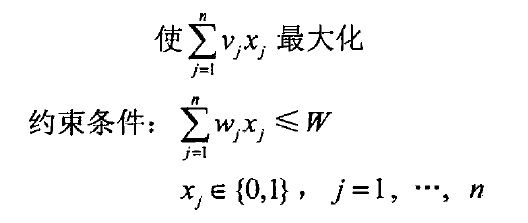
简化为图问题
许多问题可以化简为一种标准的图问题,然后再来求解。
图的顶点一般用来表示所讨论问题的可能状态,而边表示这些状态之间的可能转变。