动态规划
动态规划是求解多阶段最优决策问题的通用方法。
如果问题是由交叠的子问题构成的，我们可以用动态规划技术来解决它。
三个基本例子
-
币值最大化问题：给定一排硬币，其面值均为正整数$c_1, c_2, \cdots , c_n$ ，这些整数并不一定两两不同。请问如何选择硬币，使得在其原始位置互不相邻的条件下，所选硬币的总金额最大。
设最大可选金额为$F(n)$ ，那么：
$F(n) = max{c_n + F(n-2), F(n-1)} , n > 1$
且$F(0) = 0 , F(1) = c_1$
那么通过从左到右计算一行表格，就能够求出$F(n)$
需要耗费$\Theta(n)$时间和$\Theta(n)$ 空间。
-
找零问题：需找零金额为$n$ ，最少要用多少面值为$d_1 < d_2 < \cdots < d_m$的硬币？
设$F(n)$为总金额为$n$的数量最少的硬币的数目，定义$F(0) = 0$
递推公式：
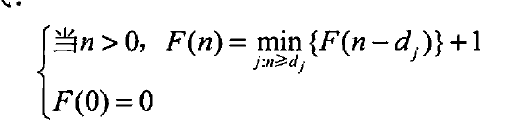
伪代码：
该算法的时间效率和空间效率显然分别是$O(nm)$和 $\Theta(n)$
- 硬币收集问题：
背包问题和记忆功能
背包问题：给定$n$个重量为$w_1, \cdots , w_n$ ，价值为 $v_1, \cdots, v_n$的物品和一个承重量为$W$的背包，
求这些物品汇总最优价值的一个子集，并且又能够装到背包中。
设计一个动态规划算法，考虑一个由前$i$个物品定义的实例，背包的承重量为$j$
$F(i,j)$为该实例的最优解的物品总价值。
可以把前$i$个物品中能够放进承重量为$j$的背包中的子集分成两个类别：
包括第$i$个物品的子集和不包括第$i$个物品的子集，然后有：
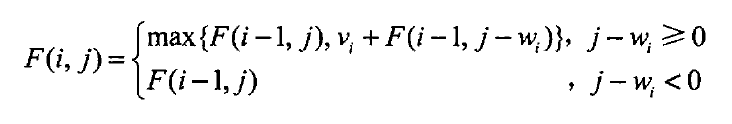
容易定义以下初始条件：
当$j \geq 0时，F(0, j) = 0 ；当 i \geq 0时 ，F(i, 0) = 0$
根据这些条件去填这么一个表格：
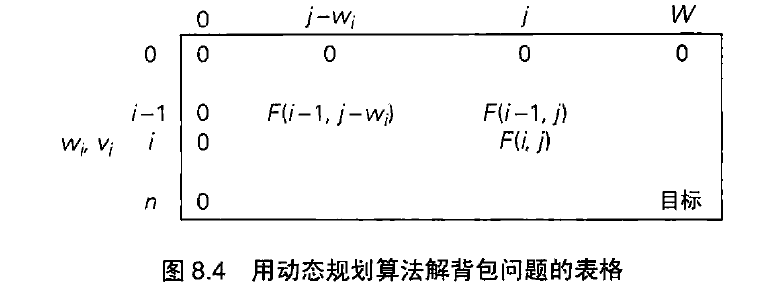时时间效率，空间效率都属于 $\Theta(nW)$
记忆化
因为动态规划方法所涉及问题的解满足一个用交叠的子问题来表示的递推关系。
直接自顶而下对这样一个递推式求解效率是十分低的，一般是指数级的。
另一方面，经典的动态规划方法是自底而上的，它用所有较小子问题的解填充表格，
但是每个子问题只解一次，但有些较小子问题的解常常不是必需的。
记忆化结合两者的优点。
它用自顶而下的方式对给定的问题求解，但还需要维护一个类似自底而上动态规划算法使用的表格。
一开始的时候，用”null”初始化这个表格，之后，若需要计算一个新的值，就先查找表格，若为”null”,
则说明还没被计算，计算之后将结果存到表格，之后若有用到，就不用再重新进行计算，直接取值。
伪代码如下：
最优二叉查找树
二叉查找树最主要的应用是实现字典，这是一种具有查找、插入和删除的元素集合。
如果元素的查找概率是已知的（可以从历史查找的统计数据得出），那么就可以引出最优二叉查找树的问题：
最优二叉查找树在查找中的平均键值比较次数是最低的。
寻找最优二叉查找树：
找递推，分解子问题，使用动态规划，填表格。
过程较复杂，思想方法还是类似的，略过了。
Warshall算法和Floyd算法
Warshall算法
一个$n$顶点的有向图的传递闭包（transitive closure）可以定义为一个$n$阶布尔矩阵，
若第$i$个顶点到第$j$个顶点之间存在一条有效的有向路径，那么矩阵的第$i$行第$j$列的元素为
1，否则为0
可以使用深度优先查找或者广度优先查找生成传递闭包，但是比较低效，对每个顶点都得遍历图。
而Warshall算法就是一个比较高效的生成传递闭包的算法。
该算法通过一系列$n$阶布尔矩阵来构造传递闭包
$R^{(0)}, \cdots, R^{(k-1)}, R^{(k)} , R^{(n)}$
每一个这种矩阵都提供了有向图中有向路径的特定信息，当且仅当从第$i$个顶点到第
$j$个顶点之间存在一条有向路径，且路径的每一个中间顶点的编号不大于$k$时，
$r_{ij}^{(k)} = 1$
易得$R^{0}$就是有向图的邻接矩阵。
该算法的中心思想是$R^{k}$中的所有元素都可以通过它在序列中的前驱$R^{(k-1)}$计算得到：
$ r_{ij}^{k} = r_{ij}^{k-1} OR (r_{ik}^{(k-1)} AND r_{kj}^{(k-1)})$
理解了这个之后 ，容易写出伪代码：
时间效率: $\Theta(n^3)$
计算完全最短路径的Floyd算法
问题定义：
给定一个加权连通图，完全最短路径问题就是要求找到从每个顶点到其他所有顶点之间的距离（最短路径的长度）。
类似Warshall算法，Floyd算法通过一系列$n$阶矩阵来计算一个$n$顶点加权图的距离矩阵：
$D^{(0)} , \cdots, D^{(k-1)}, D^{(k)}, \cdots. D^{(n)}$
矩阵$D^{k}$的第$i$行第$j$列的元素$d_{ij}^{(k)}$
表示从第$i$个顶点到第$j$个顶点之间所有路径中一条最短路径的长度，并且路径的每一个中间顶点的编号不大于$k$。
找递推：
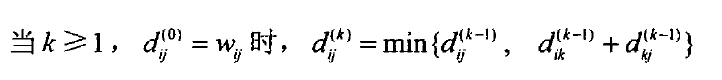
伪代码：
