本文目录
奇异值分解
奇异值分解(Singular Value Decomposition,以下简称SVD)是在机器学习领域广泛应用的算法,它不光可以用于降维算法中的特征分解,还可以用于推荐系统,以及自然语言处理等领域。是很多机器学习算法的基石。下面对SVD的数学原理做一个回顾。
特征值和特征向量
特征值和特征向量的定义如下:
\[Ax = \lambda x\]其中A是一个$m \times m$的是矩阵,$x$是一个$m$维向量,则我们说$\lambda $是矩阵A的一个特征值,而$x$是矩阵A的特征值$\lambda$对应的特征向量。
假设矩阵A的$n$个特征值 $ \lambda_1 \leq \lambda_2 \leq … \leq \lambda_ m$,且这$m$个特征值对应的$m$个线性无关的特征向量为 $ u_1, u_2, …. u_m$,假设矩阵$U = [u_1, u_2, …, u_m]$,即$U$的列向量是矩阵A的特征向量,那么由特征向量的定义有:
\[\begin{array}{l}{A U=A\left(\vec{u}_{1}, \vec{u}_{2}, \ldots, \vec{u}_{m}\right)=\left(\lambda_{1} \vec{u}_{1}, \lambda_{2} \vec{u}_{2}, \ldots, \lambda_{m} \vec{u}_{m}\right)} \\ {=\left(\vec{u}_{1}, \vec{u}_{2}, \ldots, \vec{u}_{m}\right) \left[ \begin{array}{ccc}{\lambda_{1}} & {\cdots} & {0} \\ {\vdots} & {\ddots} & {\vdots} \\ {0} & {\cdots} & {\lambda_{m}}\end{array}\right]} \\ {\Rightarrow A U=U \Lambda} & {\Rightarrow A=U \Lambda U^{-1}}\end{array}\]特别的,当矩阵A是一个实对称矩阵时,则存在一个对称对角化分解,即:
\[A = Q\Lambda Q^T\]其中,$Q$的每一列都是相互正交的特征向量(正交矩阵, 即$Q^T Q = QQ^T = I$),且都是单位向量,$\Lambda$对角线上的元素是从大到小排列的特征值(实对称矩阵必存在对角化分解)。
SVD的数学含义
SVD同样是对矩阵进行分解,但不要求矩阵$A$一定是方阵,假设矩阵$A = A_{m \times n}$ ,那么容易得到,$AA^T$的大小为$m \times m$的实对称方阵,$A^TA$的大小为$n \times n$的实对称方阵, 由上述可知,实对称方阵存在对称对角化分解,假设 $AA^T = P\Lambda_1 P ^T, A^TA = Q\Lambda_2Q^T$,则矩阵A的奇异值分解为
\[A = P\Sigma Q^T\]其中,矩阵$P=\left(\vec{p}_1,\vec{p}_2,…,\vec{p}_m\right)$的大小为$m\times m$,列向量$\vec{p}_1,\vec{p}_2,…,\vec{p}_m$是$AA^T$的特征向量,也被称为矩阵$A$的左奇异向量(left singular vector);矩阵$Q=\left(\vec{q}_1,\vec{q}_2,…,\vec{q}_n\right)$的大小为$n\times n$,列向量$\vec{q}_1,\vec{q}_2,…,\vec{q}_n$是$A^TA$的特征向量,也被称为矩阵$A$的右奇异向量(right singular vector);矩阵$\Lambda_1$大小为$m\times m$,矩阵$\Lambda_2$大小为$n\times n$,两个矩阵对角线上的非零元素相同(即矩阵$AA^T$和矩阵$A^TA$的非零特征值相同,推导过程见附录1);矩阵$\Sigma$的大小为$m\times n$,位于对角线上的元素被称为奇异值(singular value)。
证明(为什么这么取$P$和$Q$ ):
\[A=P \Sigma Q^{T} \Rightarrow A^{T}=Q \Sigma^{T} P^{T} \Rightarrow A^{T} A=Q \Sigma^{T} P^{T} P \Sigma Q^{T}=Q \Sigma^{2} Q^{T} \\ 同理可得 AA^T = P\Sigma^2P^T\]容易看出($AA^T $ 或者说是$A^TA$的)特征值矩阵等于奇异值矩阵的平方,也就是说特征值和奇异值满足以下的关系:
\[\sigma_{i}=\sqrt{\lambda_{i}}\]SVD示意图:
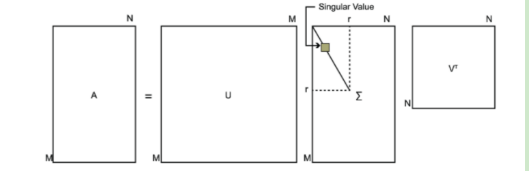
SVD的性质以及应用
对于奇异值,它跟我们特征分解中的特征值类似,在奇异值矩阵中也是按照从大到小排列,而且奇异值的减少特别的快,在很多情况下,前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上的比例。也就是说,我们也可以用最大的k个的奇异值和对应的左右奇异向量来近似描述矩阵。也就是说:
\[A_{m \times n}=P_{m \times m} \Sigma_{m \times n} Q_{n \times n}^{T} \approx P_{m \times k} \Sigma_{k \times k} Q_{k \times n}^{T}\]用低秩逼近去近似矩阵$A$有什么价值呢?给定一个很大的矩阵,大小为$m\times n$,我们需要存储的元素数量是$mn$个,当矩阵$A$的秩$k$远小于$m$和$n$,我们只需要存储$k(m+n+1)$个元素就能得到原矩阵$A$,即$k$个奇异值、$km$个左奇异向量的元素和$kn$个右奇异向量的元素;若采用一个秩$r$矩阵$A_1+A_2+…+A_r$去逼近,我们则只需要存储更少的$r(m+n+1)$个元素。因此,奇异值分解是一种重要的数据压缩方法。
由于这个重要的性质,SVD可以用于PCA降维,来做数据压缩和去噪。也可以用于推荐算法,将用户和喜好对应的矩阵做特征分解,进而得到隐含的用户需求来做推荐。同时也可以用于NLP中的算法,比如潜在语义索引(LSI)。